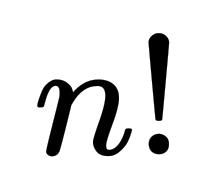Which is roughly 6.7*10^540.
You must log in or register to comment.
Better yet we make the circle 2π and then divide it such that no one knows what it means
How are there 2 πs in a circle when you only get to eat 1 π?
The Big π is lying to you you can eat 2π
but aren’t those 2π technically 4π? i’m so confused
2π (radians) is mathematically useful because one angle unit at a distance of 1 has a length of 1. It’s not intended for navigation.
Or we can switch to polor coordinates and then use this for navigation
Since angles loop back around it’s possible that 270 is equivalent to 270!. I forget the mathy term. Co-rotational?
That would really be pretty neat. A bit unlikely though, but would be fun if it landed on the exact same angle.
Yeah… Considering that 270! contains both 4 and 90 as independent factors (as there’s a x4 that has nothing to do with the x90), it means that it’s a multiple of 360. So it’s rotationally equivalent to 0.
So everything after 89!° is corotational with 0?
The bar should actually be a lot lower than that. The “90 and 4” factors just jumped out at me because the thread was already talking about 90 degree rotations. 45 and 8 would be another valid option, for example.
360 = 2x2x2x3x3x5.
With 2 and 4, all of the 2s are covered. With 3 and 6, all of the 3s are covered (and we pick up an extra 2). Then with 5, we’ve covered the whole thing. (You can see why we defined degrees to put 360 of them in a circle – lots of small factors makes it easy to slice into 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, etc parts.)
So, starting with 6!, they’re all multiples of 720, and therefore multiples of 360.
That sounds just mathy enough to be believable, and said with such confidence I don’t even need to check your work!
Thanks for the explanation.
LOL. The proposed new compass system has two norths, because apparently one just wasn’t enough.
